Introdução

Imagine que você está passando os olhos por notícias de jornal no seu celular e se depara com a seguinte chamada: “professores da escola X descobrem método de ensino que melhora desempenho dos alunos em leitura em 6.9%”. Diferentes pessoas teriam diferentes reações a ler este título, mas é inegável que a maioria iria aceitar este novo fato como verdade e seguir com suas vidas, podendo até copiar o link da matéria e compartilhar com outras pessoas (sem ler o texto completo), quando o ideal seria nos perguntarmos: como o jornalista chegou a esta conclusão?

Atrelar um número a uma conclusão passa um senso de autoridade. Ainda mais se as palavras “estatística” ou “ciência de dados” estiverem no meio. A cientista de decisão do Google Cassie Kozyrkov chama isso de viés de ciência de dados. O termo é excelente por que em meio a tanto hype em torno do uso de dados para tomada decisão, parece que salpicar um termo estatístico aqui e ali em uma apresentação ou análise automaticamente faz com a Verdade apareça. Um outro exemplo comum de viés de ciência de dados é atrelar um gráfico bonito a uma conclusão, mas que no fundo não complementa a análise ou até leva a conclusões enganosas. Eu falei um pouco disso nesse texto aqui.

Mas voltando aos números. Também ajuda na persuasão quando estes vierem com uma precisão decimal, como “6.9”, e indicarem uma mudança em relação a outro cenário. Para entender melhor, vamos olhar em mais detalhes o exemplo dos professores.

Suponha que a escola X da matéria do jornalista esteja avaliando dois programas de leitura diferentes, Programa A (o que vem sendo utilizado atualmente – o status quo em jargão estatístico) e Programa B (método novo de ensino), para determinar qual deles é mais eficaz para melhorar as habilidades de leitura dos alunos. Eles separam a turma em 2 grupos com tamanhos e perfis demográficos semelhantes. A cada grupo é aplicado seu respectivo método de ensino por um determinado período de tempo.

Depois de aplicar uma avaliação aos alunos, os professores encontram os seguintes resultados:

Programa A: Pontuação média de leitura dos alunos que participaram: 72 pontos.

Programa B: Pontuação média de leitura dos alunos que participaram: 77 pontos.

Foi de posse destas informações que o jornalista escreveu sua chamada. A diferença entre 77 e 72 é 5, que dividido por 72 é igual a 6.9%. De fato, o aumento na média é de 6.9%, mas qual é o significado prático desse aumento percentual? Podemos concluir que a turma melhorou em 6.9% só por causa do aumento médio?

A resposta é não. Identificar se ocorreu uma melhoria de fato depende também do quanto as notas variam entre os alunos, isto é, do desvio padrão da nota na turma. Isso porque a média por si só conta apenas uma parte da história por trás dos dados – no caso, qual a medida central da distribuição. É preciso complementar a medida de centralidade com uma de dispersão (o desvio padrão neste caso).

Imagine que você está planejando uma viagem e decide comparar as temperaturas médias de duas cidades para decidir qual delas visitar. Vamos considerar duas cidades hipotéticas: Cidade A e Cidade B.

• Cidade A: Temperatura média = 25°C, Desvio padrão = 1°C
• Cidade B: Temperatura média = 25°C, Desvio padrão = 10°C

À primeira vista, as temperaturas médias das duas cidades são idênticas. No entanto, ao olharmos para o desvio padrão, percebemos uma diferença significativa na variabilidade das temperaturas:

• Na Cidade A, o desvio padrão é baixo (1°C), indicando que as temperaturas tendem a ser consistentes em torno da média. Isso sugere que você provavelmente experimentará temperaturas próximas a 25°C durante a sua estadia.
• Na Cidade B, o desvio padrão é alto (10°C), o que significa que as temperaturas variam consideravelmente em relação à média. Isso poderia resultar em dias muito quentes e outros mais frios, tornando mais difícil planejar as atividades da viagem.

Nesse caso, a informação do desvio padrão ajuda a entender a dispersão das temperaturas e a tomar uma decisão mais informada sobre qual cidade visitar, além de apenas considerar a temperatura média.

Voltando ao exemplo inicial, imaginemos dois cenários para nossa escola hipotética. No primeiro, o desvio padrão da turma é de 20 pontos (estamos olhando apenas para o nosso status quo; sendo assim, a nossa nota média dos alunos em ambos os cenários a seguir mantêm-se no valor inicial de 72). Em seguida vamos imaginar um segundo cenário, em que o desvio padrão da turma é de 5 pontos. Para colocar a diferença entre os cenários em perspectiva vamos visualizar em um gráfico a distribuição das notas dos alunos de ambos os cenários usando um histograma.

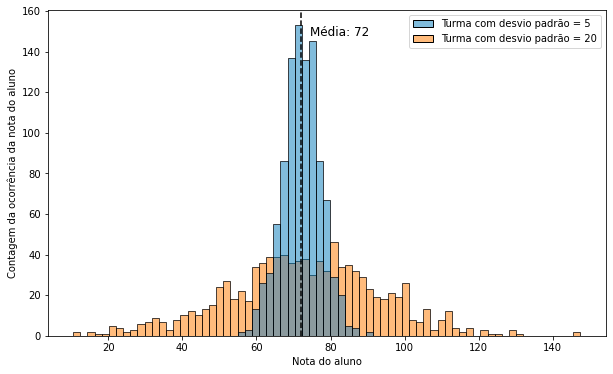
Colocando as duas distribuições lado a lado fica bem clara a diferença: a turma com desvio padrão igual a 5, em azul, é mais nivelada, isto é, o nível de leitura dos alunos é muito parecido entre si. Quase não há casos de alunos que tiram notas muito baixas, nem casos de alunos que gabaritam o exame. 95% dos alunos tem nota entre 62 e 82¹.

Então qual seria a maneira mais correta de identificar se o aumento na média é significativo?

Aqui precisaremos nos valer do conceito de percentil. O percentil nos diz, referente a uma distribuição de dados, qual é o ranking de um determinado valor dentro dessa distribuição em uma escala de 0 a 100%. Para calcularmos o percentil, organizamos todos os valores em ordem crescente e verificamos como um valor específico se posiciona em relação aos demais. Por exemplo, em uma turma de 100 alunos, se a nota do aluno João é maior do que a de 85 colegas, então João está no percentil 85. Em outras palavras, João tem melhor nota do que 85% da sala.

Como usar o desvio padrão e percentil para identificarmos se a melhoria no desempenho médio da turma é significativo

Vamos alterar nosso exemplo inicial para utilizar valores mais extremos para fins de clareza. Vamos imaginar que o aumento médio na média das turmas com diferentes métodos de ensino tenha passado de 72 para 90, ao invés de 77:

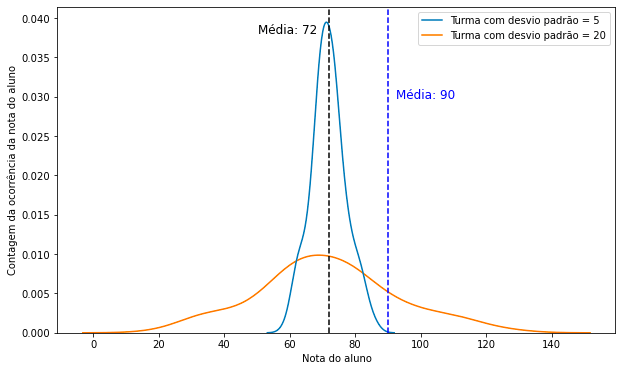
Para a turma com desvio padrão igual a 5, um aluno com nota 72 estaria no percentil 52, ou seja, na média², ao passo que com nota média de 90 seria o melhor aluno da sala, estando no percentil 100. Já um aluno com a mesma nota sairia do percentil 52 para 80 na turma com desvio padrão 20. Agora temos uma métrica de comparação mais adequada. Se temos um aluno que tem desempenho igual à média com um método de ensino e que passa a desempenhar como melhor da turma com o método novo, então passa a fazer sentido afirmar que o método de ensino é efetivo.

A métrica que quantifica a melhoria entre 2 cenários

Existe uma métrica que condensa em um único número a análise feita anteriormente quando estudamos a diferença no efeito entre 2 cenários que se chama tamanho do efeito (do inglês effect size). E que leva em conta a média e o desvio padrão das amostras e nos dá uma métrica padronizada, que nos permite comparar tratamentos distintos. Sem entrar em detalhes técnicos aprofundados, que não é o objetivo deste texto, para o exemplo inicial podemos usar o método de Cohen’s d, cuja interpretação nos permite afirmar que:

• Tamanho de efeito pequeno assume valores ao redor de 0.2
• Tamanho de efeito médio assume valores ao redor de 0.5
• Tamanho de efeito grandes assumem valores acima de 0.8

Aplicando o método de Cohen’s d para nosso exemplo da escola, temos que para a turma com desvio padrão igual a 20, o tamanho do efeito é de 0.24, ou seja de pequeno efeito. Em outras palavras, isso indica que a diferença entre os dois programas, embora possa ser estatisticamente significativa, pode não ter um impacto prático substancial na melhoria das habilidades de leitura dos alunos. Já para a turma com desvio padrão igual a 5, o tamanho do efeito é de 0.96, ou seja, grande, indicando melhoria na habilidade de leitura.

Esta é a mensagem fundamental deste texto: as duas turmas com desvios padrões diferentes saíram de médias 72 para 77 com os métodos novos de ensino atingindo 6.9% de melhoria na média; mas apenas para a turma com desvio padrão menor o tamanho do efeito foi significativo. A explicação pode ser melhor compreendida utilzando os percentis novamente: um aluno que sai de média 72 para 77 na turma de desvio padrão 5 sai do percentil 52 para 82, ao passo que na para a turma de desvio padrão 20 o mesmo resultado levaria o aluno do percentil 52 para o 64. A grande lição aqui é: devemos tomar cuidado com a simplificação de análises estatísticas ao olhar apenas para uma métrica. Nosso cérebro tem uma tendência natural a aceitar melhor as informações que vem com números embasando-as, mas não necessariamente a conclusão que a pessoa fazendo a análise fez é correta. Na era de redes sociais em que cada vez mais consumimos informações pelas manchetes ao invés ler os textos inteiros e simplesmente aceitando o argumento de autoridade sem saber quem está do outro lado do texto, este risco torna-se cada vez maior.

Notas de rodapé

¹ Para facilitar a didática, estou assumindo que a distribuição das notas dos alunos segue uma distribuição normal. Como sabemos desta distribuição, 95% dos dados encontram-se entre +/- 2 desvios padrões da média.

2 Como a distribuição das notas segue uma normal, a média é igual à mediana.