Introdução

Imagine uma cidade em que há dois hospitais. O primeiro deles, maior, registra, em média, 100 nascimentos de bebês por dia. O segundo, menor, registra 15. Considerando que a probabilidade de gestar um bebê tanto do sexo masculino quanto do feminino seja de 50%, em qual dos hospitais é mais provável acontecer dias em que nasçam 60% ou mais de meninos?

A maioria das pessoas tende a achar que não há diferença, ou até que o hospital maior tende a ter maior número de bebês do sexo masculino. Em ambos os casos a resposta está incorreta. A teoria matemática que ajuda a explicar o porquê é denominada lei dos grandes números.

Sobre valor esperado e apostar em dados e moedas

Para entender melhor a lei dos grandes números, entretanto, precisamos introduzir um outro conceito: valor esperado.

O conceito de valor esperado em estatística pode ser comparado a uma previsão do que você espera ganhar ou perder, em média, ao realizar uma ação muitas vezes. Imagine, por exemplo, que você tem um dado justo de seis lados, e você ganha o número de reais correspondente ao número que sai no dado cada vez que você joga. O valor esperado nos diz quanto de dinheiro, em média, você pode esperar ganhar.

Elaborando o exemplo: sabendo que cada face do dado tem a mesma chance de sair, ou seja, 1 em 6. Se você multiplicar cada possível resultado (1, 2, 3, 4, 5, 6) pela sua probabilidade de acontecer (1/6), e somar todos esses valores, você terá o valor esperado.

Então, para o dado, o cálculo seria: (1/6) * R$ 1,0 + (1/6) * R$ 2,0 + (1/6) * R$ 3,0 + (1/6) * R$ 4,0 + (1/6) * R$ 5,0 + (1/6) * R$ 6,0. Esse cálculo dá a média de dinheiro que você pode esperar ganhar por jogada ao longo do tempo, que é igual a R$3,50.

A definição genérica e mais rigorosa de valor esperado é: medida estatística que mostra o resultado médio de uma série de eventos, ponderados por suas probabilidades de ocorrência.

Nos parágrafos acima a frase “em média, ao realizar uma ação muitas vezes” foi colocada em negrito por que essa ideia é a chave para o entendimento. Frente a situações que são sujeitas a probabilidade (também conhecido como processo estocástico), incerteza e aleatoriedade, o valor esperado nos dá uma métrica para uma tomada de decisão mais informada.

Para o exemplo do dado, sabendo-se que o valor esperado de apostar no número da face do dado é de R$3,5, essa informação agora pode embasar a decisão de apostar ou não caso alguém te informe o custo deste jogo. Se o custo de jogar for de R$ 3,0, vale a pena arriscar. Se o custo for de qualquer valor acima de R$ 3,5, não.

Mas lembre-se: isso é o valor médio se o dado for jogado várias vezes. Se você jogar o dado apenas 1 vez, é muito pouco. E é neste aspecto que a lei dos grandes números entra em cena.

Entendendo a lei dos grandes números

A Lei dos Grandes Números é um princípio fundamental em probabilidade e estatística que descreve o resultado de realizar o mesmo experimento muitas vezes. Segundo essa lei, quanto mais vezes o experimento é realizado, mais a média dos resultados obtidos se aproximará do valor esperado teórico. Em outras palavras, a Lei dos Grandes Números nos diz que a estatística e a probabilidade funcionam bem juntas a longo prazo. E isso é a base teórica fundamental da vertente chamada Frequentista da Estatística (a outra é a Bayesiana).

Por exemplo, se você jogar uma moeda justa (50% de chance de cara, 50% de chance de coroa) algumas vezes, é possível obter uma sequência como cara, cara, coroa, cara, o que não reflete exatamente a probabilidade de 50/50. No entanto, se você continuar jogando essa moeda, digamos, milhares ou milhões de vezes, verá que o número de caras e coroas se aproxima cada vez mais de uma divisão 50/50.

Vejamos isto na prática. Simulando 15 jogadas de moeda temos o gráfico a seguir: nele podemos ver a elevada variabilidade inerente a uma amostra pequena. O valor esperado teórico é termos 50% (0.5 no eixo y do gráfico) de resultados de cara. Mas nota-se que com um baixo número de jogos esse valor é atingido poucas vezes, alem de termos elevada variabilidade.

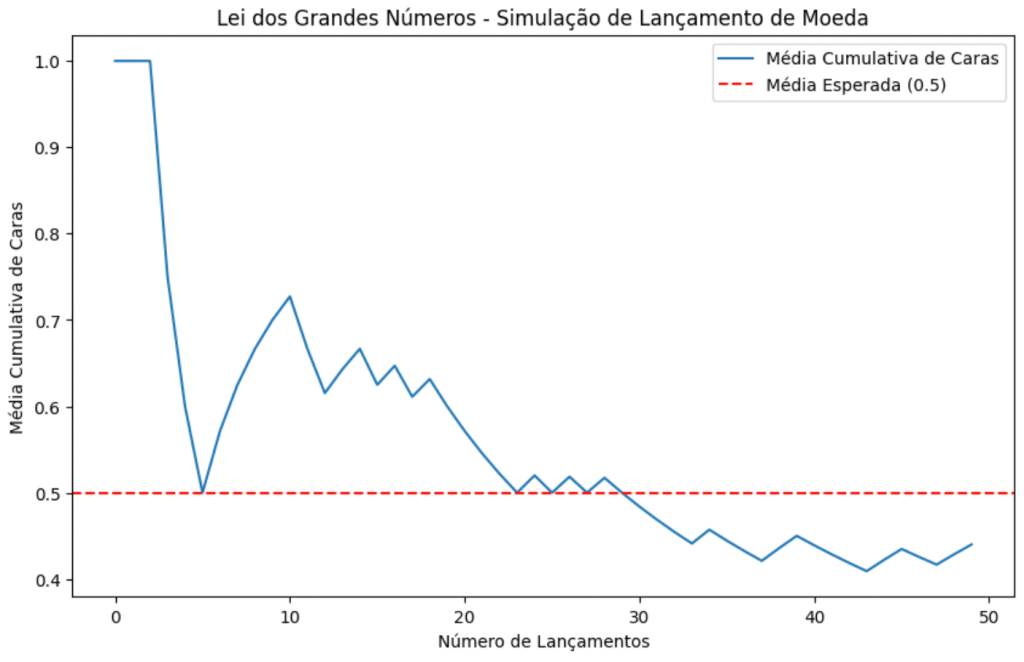
Vejamos agora a simulação com 10.000 jogos da moeda:

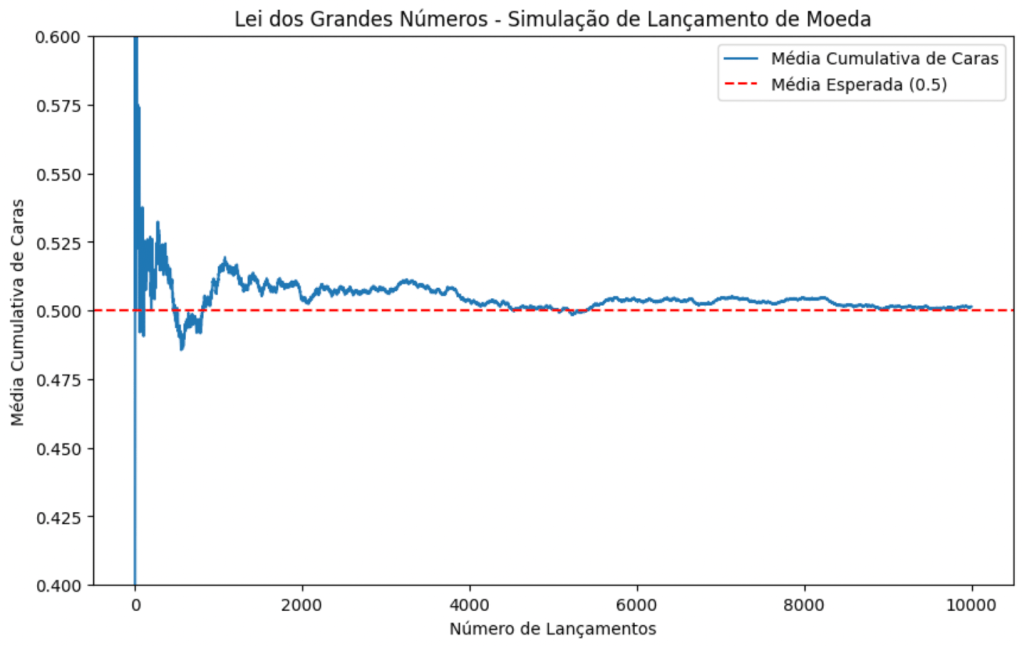
Aqui fica clara a força da lei dos grandes números. Com um número suficientemente alto de jogos, a média de resultados obtidos de cara ficou, quando não exatamente igual, muito próximo do valor teórico e com baixa variabilidade.

O ponto crucial a entender é que a Lei dos Grandes Números é a razão pela qual as médias de longo prazo se tornam previsíveis e estáveis, apesar da aleatoriedade e da variação de curto prazo. Este conceito serve de base para muitos aspectos da ciência, economia, e até mesmo para o dia a dia, como entender que um cassino sempre tem vantagem a longo prazo, não importa o quanto alguém possa ganhar em uma noite, bem como nosso exemplo inicial dos hospitais e o nascimento de bebês do sexo masculino.

Por que os cassinos sempre ganham e por que é uma má ideia apostar na mega-sena

Para entender por que os cassinos sempre ganham, vamos usar o jogo da roleta francesa como exemplo. Neste jogo existem 37 casas numeradas. Os jogadores podem apostar em qualquer uma delas, exceto na casa de número 0. Quando a bola para nessa casa, o dinheiro vai para o cassino.

Se você apostar em um único número, as chances de ganhar são de 1 em 37, pois há apenas uma casa vencedora e 36 casas perdedoras.

Quando você ganha ao apostar em um único número, o pagamento é de 35 para 1. Isso significa que, para cada unidade de moeda apostada, você recebe de volta 36 unidades (seu ganho de 35 unidades mais a unidade original que você apostou). No entanto, se a bola cair na casa 0, todas as apostas em números perdem.

Vamos calcular o valor esperado de fazer uma aposta de 1 unidade monetária em um único número.

• Probabilidade de ganhar (P(ganhar)): 1/37
• Probabilidade de perder (P(perder)): 36/37
• Ganho se vencer: 35 unidades (pois você recupera sua aposta e ganha mais 35 unidades)
• Perda se perder: -1 unidade (você perde sua aposta)

O valor esperado (E) é calculado como a soma dos produtos das probabilidades de cada resultado pelo seu valor correspondente. Matematicamente:

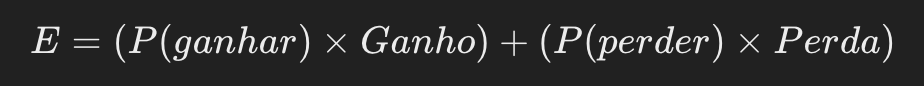
Substituindo os valores:

O que resulta em, aproximadamente, -2,7%. Este valor negativo indica que o valor esperado desse jogo sempre irá desfavorecer o jogador. Só que a elevada variabilidade atrelada a pequenas amostras faz com que alguns jogadores ganhem em algumas ocasiões. Mas pense sob a perspectiva do cassino: são milhares de jogadores que, a longo prazo, garantirão que, na média, o cassino tenha um valor esperado de 2,7 (positivo, pois estamos sob a perspectiva do cassino agora). Ou seja, (muito) lucro. Mesmo que isso se dê às custas de alguns jogadores ganhando muito.

Se quiser pensar visualmente sobre a explicação último parágrafo, imagine que a perspectiva do apostador é a da Figura 1 – imprevisibilidade, elevada variabilidade, em que o valor esperado em alguns casos é atingido e até superado, mas em outros o valor esperado fica bem abaixo também. A perspectiva do cassino é da Figura 2: o elevado número de apostadores e jogos garante previsibilidade de que o valor esperado será atingido.

Eventualmente alguns jogadores ganharem é benéfico ao cassino pois alimenta o imaginário de jogadores e apostadores através da falácia do apostador. Este é um erro de raciocínio comum em jogos de azar e em outras situações que envolvem probabilidades. Ela ocorre quando uma pessoa acredita que eventos passados podem influenciar o resultado de um evento futuro, apesar de os eventos serem independentes entre si. Um exemplo clássico é pensar que, após uma sequência de “caras” no lançamento de uma moeda, há uma maior probabilidade de que o próximo lançamento resulte em “coroa”, para “equilibrar” os resultados. Na realidade, a probabilidade de obter cara ou coroa em cada lançamento é sempre de 50%, independentemente dos lançamentos anteriores.

Essa falácia é chamada assim porque é particularmente prevalente entre apostadores, que podem acreditar, por exemplo, que estão “destinados” a ganhar após uma sequência de perdas. No contexto de um cassino, um jogador pode pensar que uma máquina caça-níqueis está “quente” ou “fria” baseado nos resultados anteriores, o que o leva a acreditar erroneamente que pode prever os próximos resultados.

Com relação à mega-sena, o raciocínio é análogo. O valor esperado (VE) de ganhar o prêmio é calculado como sendo:

VE=(Probabilidade de ganhar×Valor do prêmio)−Custo da aposta

Em que a probabilidade de ganhar é 1 em 50.063.860 (combinação de 60 números tomados 6 a 6). Além disso, considerando que um bilhete custa R$ 5,0 e um prêmio hipotético de R$50.000.000, o valor esperado é de R$-4,0. Novamente um valor negativo.

Conclusão

A ideia chave deste texto é entender que, para eventos que tem um componente de aleatoriedade e probabilidade envolvidos, a lei dos grandes números se aplicará e o valor esperado de proporções (percentuais, médias, medianas, etc) se aproximará do valor esperado quanto maior for o tamanho da amostra. Amostras pequenas sempre estarão mais sujeitas a aleatoriedade e variação de curto prazo. Voltando ao exemplo inicial dos hospitais, a resposta correta é: o hospital menor está sujeito a ter nascimentos de 60% ou mais de bebês do sexo masculino, justamente por menos partos serem realizados (menor amostra), tornando-o mais suscetível à variabilidade de curto prazo.

Este é outro exemplo em que podemos nos valer de simulação para provar. Para uma sequência de 100 dias, a probabilidade de nascer 60% ou mais de meninos no hospital pequeno é de 24%, ao passo que no hospital maior é de 3%.